ไม่ได้ส่งคำตอบ
0.0
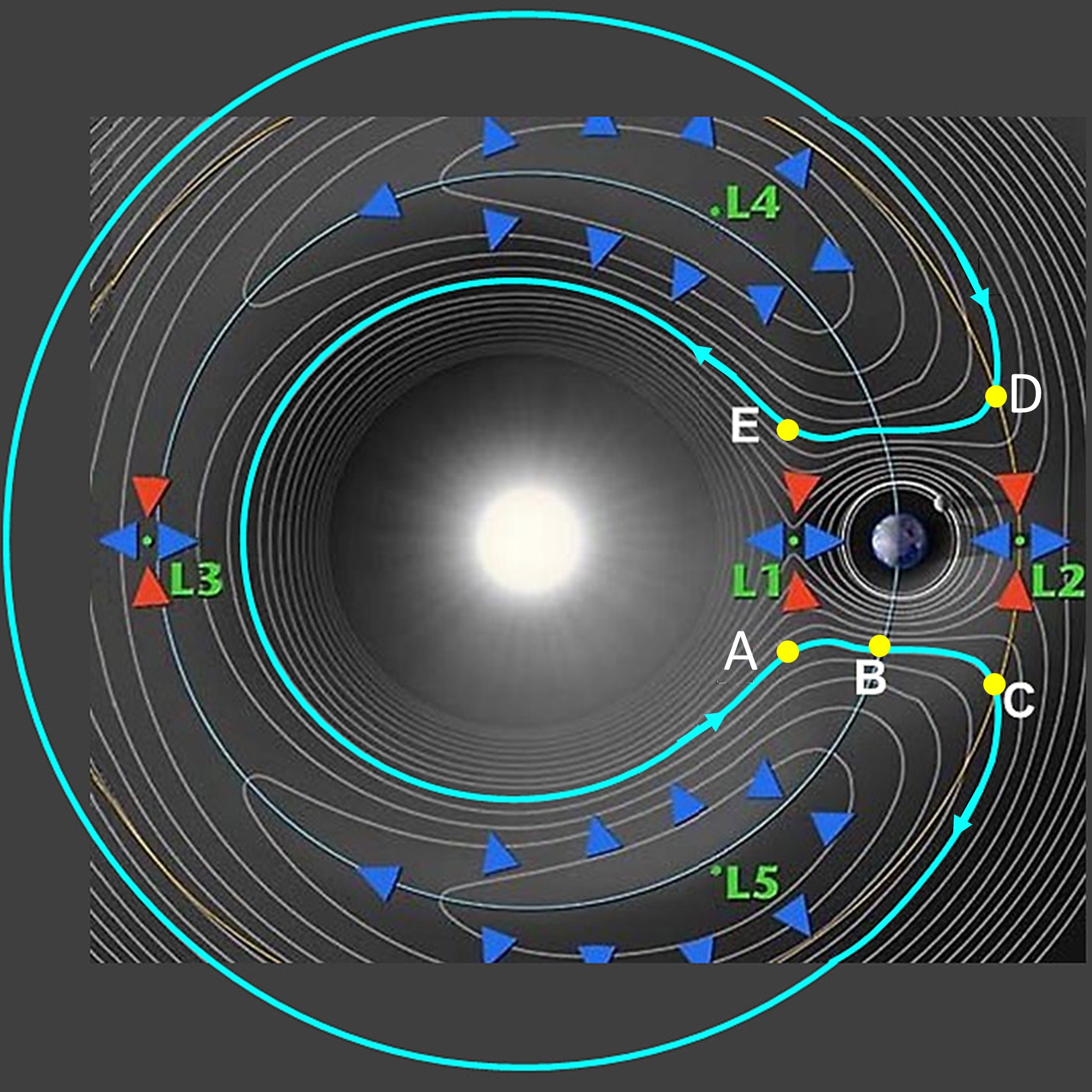
รูปด้านล่างแสดงลักษณะวงโคจรอย่างคร่าวๆ พร้อมกับจุด Lagrange point ของระบบดวงอาทิตย์และโลก วัตถุมีทิศการเคลื่อนที่ (เทียบกับโลก) จาก A->B->C->D->E แล้วกลับมา A
ให้ถือว่าวัตถุในวงโคจรนี้อยู่ภายใต้แรงโน้มถ่วงของดวงอาทิตย์เป็นหลัก และได้ได้รับอิทธิพลจากแรงโน้มถ่วงของโลกเมื่ออยู่ใกล้โลกเท่านั้น (บริเวณ จุด A B C D E)
ให้ถือว่าวงโคจรทั้งนอกและในเป็นส่วนส่วนหนึ่งของวงกลม มีเฉพาะบริเวณจุด A C D E เท่านั้นที่เปลี่ยนการเคลื่อนที่
ให้ $L$ เป็นระยะจากโลกไปยังจุด L1 (ซึ่งประมาณเท่ากับระยะจากโลกไปยังจุด L2)
ให้ $R$ เป็นระยะจากดวงอาทิตย์ไปยังโลก
ให้ประมาณว่า ระยะจากจุด A, B, C, D, E ไปยังโลก มีขนาดใกล้เคียงกับ $L$ และการเคลื่อนที่จาก A->B->C หรือจาก D->E ใช้เวลา 1 - 2 เดือนเท่านั้น
มวลของโลก $M_E = 5.97 \times 10^{24} \ \text{kg}$
มวลดวงอาทิตย์ $M_S = 1.99 \times 10^{30} \ \text{kg}$
ระยะจากโลกไปดวงอาทิตย์ $R = 1.50 \times 10^{11} \text{m}$
และ $L = 0.010R$
ค่าคงตัวแรงโน้มถ่วงสากล $G = 6.67 \times 10^{-11} \ \text{Nkg}^{-2}\text{m}^2$
จงประมาณว่าวัตถุโคจรจาก A->B->C->D->E แล้วกลับมา A วนไป ใช้เวลานานประมาณกี่ทศวรรษ (ในมุมมองของโลก) โดยให้ปัดเศษขึ้น เช่น หากนักเรียนคำนวณได้ 18 ปี ปัดขึ้นเป็น 2 ทศวรรษ ให้กรอกเลข 2
หมายเหตุ: รูปไม่ถูกต้องตามสเกล ระยะ $L$ น้อยมากเทียบกับ $R$
ตอบ 14 ทศวรรษ
คำอธิบาย
จากกฎของเคปเลอร์ คาบของโลก $P_R = \displaystyle\sqrt[]{\frac{4\pi^2R^3}{GM_S}} = 1.000$ year
สมมุติว่าวัตถุโคจรเป็นวงกลมที่มันรัศมีเท่ากับระยะจากดวงอาทิตย์ไปยังจุด $L1$
คาบเท่ากับ $P_{L1} = \displaystyle\sqrt[]{\frac{4\pi^2(R - L)^3}{GM_S}} = \displaystyle\sqrt[]{\frac{4\pi R^3 \times 0.99^3}{GM_S}} = 0.9850$ year
ให้ $T_1$ เป็นเวลาที่วัตถุโคจรจาก E มายัง A
จะได้ $\displaystyle{\frac{1}{T_1} = \frac{1}{P_{L1}} - \frac{1}{P_R}}$ หรือ $T_1$ = 65.7 ปี
สมมุติว่าวัตถุโคจรเป็นวงกลมที่มันรัศมีเท่ากับระยะจากดวงอาทิตย์ไปยังจุด $L2$
คาบเท่ากับ $P_{L2} = \displaystyle\sqrt[]{\frac{4\pi^2(R + L)^3}{GM_S}} = \displaystyle\sqrt[]{\frac{4\pi R^3 \times 1.01^3}{GM_S}} = 1.0150$ year
ให้ $T_2$ เป็นเวลาที่วัตถุโคจรจาก C มายัง D
จะได้ $\displaystyle{\frac{1}{T_2} = \frac{1}{P_R} - \frac{1}{P_{L2}}}$ หรือ $T_2$ = 67.6 ปี
ดังนั้นเวลารวมเท่ากัน 133 ปี หรือประมาณ 14 ทศวรรษ
ไม่ต้องคำนึงถึงส่วนของวงกลมที่หายไป หรือการเคลื่อนที่จาก A->B->C เพราะมีค่าน้อยมาก