ข้อที่ 41

ตอบ 3)

จาก $s=v_1+\frac{1}{2}at^2$ และ $s=\frac{(v_1+v_2)}{2}t$

1)  $a$ มากที่สุดเมื่อ $v_1\rightarrow 0$ ซึ่งจะได้ว่า $a \lt 4.00 \: \textrm{m}/\textrm {s}^2$

2) $v_1=\frac{s}{t}-\frac{1}{2}at$ ซึ่งมีค่ามากสุดเมื่อ $a \rightarrow 0$ หรือ $v_1 \rightarrow 10.0 \: \textrm{m/s}$

3) $v_2$ มากที่สุดเมื่อ $v_1 \rightarrow 0$ ซึ่งได้ว่า $v_2 \lt 20.0 \: \textrm{m/s}$

4) แทนค่าจะเห็นว่าเป็นคำตอบที่ถูกต้อง

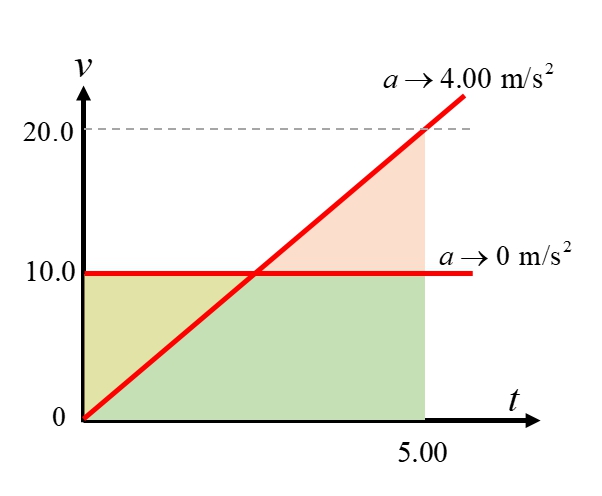
หรือพิจารณาจากกราฟข้างล่างนี้ โดยพื้นที่ใต้กราฟต้องเท่ากับ $50.0 \: \textrm{m}$ พอดี