คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
ไม่ได้ส่งคำตอบ 
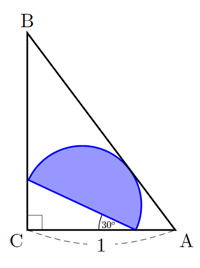
$\Delta\text{ABC}$ มี $\hat{\text{B}} = 30^{\circ}, \hat{\text{C}} = 90^{\circ}, \text{AC} = 1$ หน่วย มีครึ่งวงกลมแนบใน $\Delta\text{ABC}$ โดยเส้นผ่านศูนย์กลางทำมุม $30^{\circ}$ กับ $\overline{\text{AC}}$ ดังรูป
สมมุติว่าครึ่งวงกลมมีพื้นที่ $\frac{a}{b}\pi$ ตารางหน่วย โดย $\frac{a}{b}$ อยู่ในรูปเศษส่วนอย่างต่ำ
จงหาค่าของ $a^2 + b^2$
สมมุติว่าครึ่งวงกลมมีพื้นที่ $\frac{a}{b}\pi$ ตารางหน่วย โดย $\frac{a}{b}$ อยู่ในรูปเศษส่วนอย่างต่ำ
จงหาค่าของ $a^2 + b^2$
เฉลย
ตอบ 1033
แนวคิด
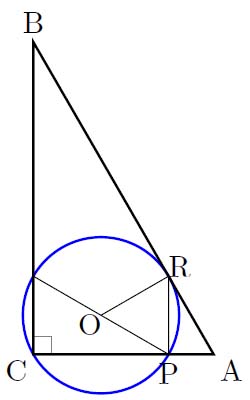
ให้ \(r\) เป็นรัศมีของครึ่งวงกลม
\(\angle\text{POR} = 360^{\circ} - \angle\text{OPA} - \angle\text{RAP} - \angle\text{ORA} = 60^{\circ}\)
\(\therefore \Delta\text{POR}\) เป็นรูปสามเหลี่ยมด้านเท่า
จึงได้ว่า \(\text{PR} = r\) และ \(\overline{\text{RP}} \bot \overline{\text{CA}} \)
\(\text{AP} = 1 - 2r \cos 30^\circ = 1 - r\sqrt[]{3}\)
\(\text{AC} \cdot \text{AP} = \text{AR}^2 = \text{PR}^2 + \text{AP}^2\)
\(1 \cdot (1 - r\sqrt[]{3}) = r^2 + (1 - r\sqrt[]{3})^2\)
\(\therefore r = \frac{\sqrt[]{3}}{4}\) และพื้นที่ครึ่งวงกลมเท่ากับ \(\frac{3}{32}\pi\)