คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
ไม่ได้ส่งคำตอบ 
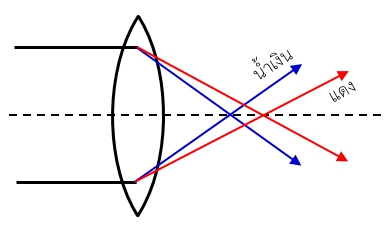
เลนส์ที่ทำจากวัสดุโปร่งแสงโดยทั่วไปมีดัชนีหักเหที่ขึ้นอยู่กับความยาวคลื่น ดังนั้นแสงแต่ละความยาวคลื่นที่เดินทางผ่านเลนส์จึงมีระยะโฟกัสที่ไม่เท่ากัน ดังแสดงเป็นตัวอย่าง (แสดง 2 สี) ในรูปข้างล่าง ปรากฏการณ์นี้เรียกว่าความคลาดสี (Chromatic Aberration)
เลนส์นูนอันหนึ่งทำมาจากแก้วที่มีดัชนีหักเหของสีต่างๆ ดังต่อไปนี้
สีน้ำเงิน $n_B=1.52541$
สีเหลือง $n_Y=1.51975$
สีแดง $n_R=1.51725$
เลนส์นี้ถูกออกแบบให้ความยาวโฟกัสของแสงสีเหลืองเท่ากับ $f_Y=20$ $\textrm{cm}$ โดยใช้สมการช่างทำเลนส์ (Lensmaker’s Equation) $\frac{1}{f} = (n-1)(\frac{1}{R_1}-\frac{1}{R_2})$ เมื่อ $f$ เป็นความยาวโฟกัสของแสงที่มีดัชนีหักเห $n$ และ $R_1$, $R_2$ เป็นรัศมีความโค้งของผิวเลนส์แต่ละด้าน
จงหาว่า ความยาวโฟกัสของแสงสีแดงและแสงสีน้ำเงิน มีค่าต่างกันกี่มิลลิเมตร ให้ตอบเป็นตัวเลขทศนิยม 1 ตำแหน่ง
หมายเหตุ: ไม่ต้องระบุหน่วยในช่องกรอกคำตอบ เช่น หากนักเรียนคำนวณได้ 0.2 มิลลิเมตร ให้กรอกเฉพาะ 0.2 เท่านั้น
เลนส์นูนอันหนึ่งทำมาจากแก้วที่มีดัชนีหักเหของสีต่างๆ ดังต่อไปนี้
สีน้ำเงิน $n_B=1.52541$
สีเหลือง $n_Y=1.51975$
สีแดง $n_R=1.51725$
เลนส์นี้ถูกออกแบบให้ความยาวโฟกัสของแสงสีเหลืองเท่ากับ $f_Y=20$ $\textrm{cm}$ โดยใช้สมการช่างทำเลนส์ (Lensmaker’s Equation) $\frac{1}{f} = (n-1)(\frac{1}{R_1}-\frac{1}{R_2})$ เมื่อ $f$ เป็นความยาวโฟกัสของแสงที่มีดัชนีหักเห $n$ และ $R_1$, $R_2$ เป็นรัศมีความโค้งของผิวเลนส์แต่ละด้าน
จงหาว่า ความยาวโฟกัสของแสงสีแดงและแสงสีน้ำเงิน มีค่าต่างกันกี่มิลลิเมตร ให้ตอบเป็นตัวเลขทศนิยม 1 ตำแหน่ง
หมายเหตุ: ไม่ต้องระบุหน่วยในช่องกรอกคำตอบ เช่น หากนักเรียนคำนวณได้ 0.2 มิลลิเมตร ให้กรอกเฉพาะ 0.2 เท่านั้น
เฉลย
ตอบ 3.1
วิธีที่ 1:
สีเหลือง $\frac{1}{f_Y} = (n_Y-1)(\frac{1}{R_1}-\frac{1}{R_2})$
สีน้ำเงิน $\frac{1}{f_B} = (n_B-1)(\frac{1}{R_1}-\frac{1}{R_2})$
สีแดง $\frac{1}{f_R} = (n_R-1)(\frac{1}{R_1}-\frac{1}{R_2})$
ตัดตัวแปรรัศมีออก จะได้
$\Delta f = f_R-f_B = f_Y((\frac{n_Y-1}{n_R-1})-(\frac{n_Y-1}{n_B-1})) = 3.1$ $\textrm {mm}$
วิธีที่ 2:
ใช้การประมาณเชิงเส้นจากสมการช่างทำเลนส์
(นักเรียนควรพึงระวัง วิธีนี้จะทำให้ทศนิยมตำแหน่งที่ 2 ผิด ซึ่งถ้าเป็นโจทย์ที่ต้องการความละเอียดมากๆ จะทำให้คำตอบผิด)
$\Delta f \approx (\frac{\Delta n}{n-1})f$
ประมาณค่ารอบแสงสีเหลือง
$\Delta f \approx f_B-f_R \approx (\frac{n_B-n_R}{n_Y-1})f_Y \approx 3.1$ $\textrm{mm}$