คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
แชร์
ไม่ได้ส่งคำตอบ 
วางมวล $4M$ และ $M$ ที่ปลายสปริงที่ถูกบีบอัดอยู่บนพื้นระนาบลื่น ในตอนเริ่มต้นมวลทั้งหมดอยู่นิ่ง เมื่อปล่อยให้ระบบเคลื่อนที่ สปริงจะคลายตัวและดันมวลให้เคลื่อนที่ออกจากกันและแยกออกจากปลายสปริง
กำหนดให้อัตราเร็วสุดท้ายของมวล $4M$ เท่ากับ $V$ เทียบกับพื้น และอัตราเร็วเฉลี่ยของสปริงทั้งอันหลังคลายตัวเท่ากับ $\alpha V$ เทียบกับพื้น
จงหาค่าของ $\alpha$ เป็นตัวเลขทศนิยม 1 ตำแหน่ง กำหนดให้สปริงไม่มีมวล (หรือมวลน้อยมากๆ เทียบกับ $M$) และสปริงยืดหดอย่างสม่ำเสมอทั้งอัน
กำหนดให้อัตราเร็วสุดท้ายของมวล $4M$ เท่ากับ $V$ เทียบกับพื้น และอัตราเร็วเฉลี่ยของสปริงทั้งอันหลังคลายตัวเท่ากับ $\alpha V$ เทียบกับพื้น
จงหาค่าของ $\alpha$ เป็นตัวเลขทศนิยม 1 ตำแหน่ง กำหนดให้สปริงไม่มีมวล (หรือมวลน้อยมากๆ เทียบกับ $M$) และสปริงยืดหดอย่างสม่ำเสมอทั้งอัน
เฉลย
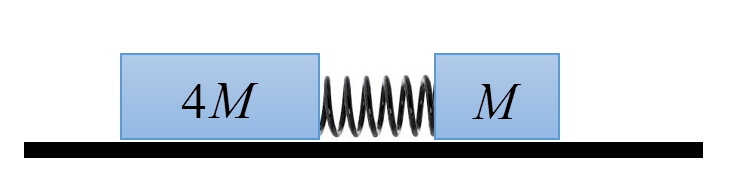
ตอบ 1.5
มวล $M$ ต้องเคลื่อนที่ด้วยอัตราเร็ว $4V$ ไปด้านขวาตามการอนุรักษ์โมเมนตัม
กำหนดให้ $u$ เป็นอัตราเร็วของจุดศูนย์กลางสปริงเทียบกับพื้น ผู้สังเกตที่ติดไปกับจุดกึ่งกลางสปริงจะต้องเห็นอัตราเร็วของปลายทั้งสองด้านเท่ากัน (เนื่องจากสปริงยืดหดอย่างสม่ำเสมอทั้งอัน)
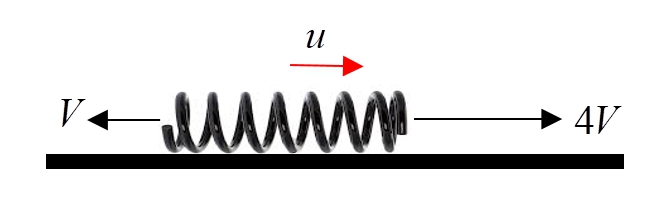
ดังนั้น จากความเร็วสัมพัทธ์ระหว่างจุดกึ่งกลางและปลายทั้งสองข้าง (ขณะที่สปริงยืดมาเท่าความยาวธรรมชาติ)
$4V-u=u+V$ หรือ $u=\frac{3}{2}V$
(หรือคิดจากความเร็วเฉลี่ยของปลายทั้งสองด้านก็ได้เท่ากัน)
หมายเหตุ:
สำหรับสปริง อัตราเร็วเฉลี่ยสุดท้ายเหมือนกับความเร็วเฉลี่ย เพราะเมื่อยืดเท่าความยาวธรรมชาติ สปริงด้านปลายซ้ายจะโดนกระชากไปทางขวา และสปริงด้านปลายขวาจะโดนกระชากให้ช้าลง สปริงทั้งอันจะมีความเร็วเท่ากันทันทีในตอนสุดท้ายเนื่องจากมันไม่มวล