คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
ไม่ได้ส่งคำตอบ 
โจทย์ข้อนี้ คล้ายข้อก่อนนี้ ต่างกันที่สปริงมีมวล
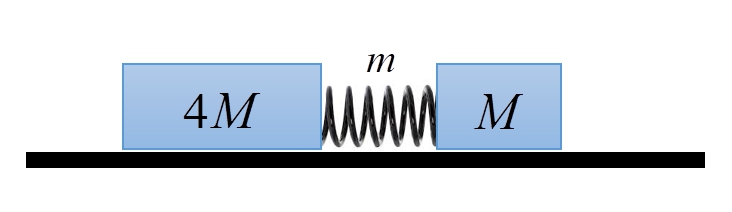
วางมวล $4M$ และ $M$ ที่ปลายสปริงที่ถูกบีบอัดอยู่บนพื้นระนาบลื่น มวลของสปริงเท่ากับ $m$ โดยที่ $m \lt M$ และในตอนเริ่มต้นมวลทั้งหมดอยู่นิ่ง เมื่อปล่อยให้ระบบเคลื่อนที่ สปริงจะคลายตัวและดันมวลให้เคลื่อนที่ออกจากกันและแยกออกจากปลายสปริง
กำหนดให้อัตราเร็วสุดท้ายของมวล $4M$ เท่ากับ $V$ เทียบกับพื้น และความเร็วเฉลี่ยของสปริงทั้งอันหลังคลายตัวเท่ากับ $u=\frac{aM}{bm+M}V$ เทียบกับพื้น
จงหาค่าของ $a$ และ $b$ เป็นตัวเลขทศนิยม 1 ตำแหน่ง โดยใช้จุลภาคคั่นระหว่างคำตอบทั้งสอง เช่น หากได้ $a=0.1$ และ $b=0.2$ ให้ตอบเป็น 0.1,0.2 ให้ประมาณว่าสปริงยืดหดอย่างสม่ำเสมอทั้งอัน อย่าลืมจัดรูปสมการให้ได้สัมประสิทธิ์ที่ต้องการ
วางมวล $4M$ และ $M$ ที่ปลายสปริงที่ถูกบีบอัดอยู่บนพื้นระนาบลื่น มวลของสปริงเท่ากับ $m$ โดยที่ $m \lt M$ และในตอนเริ่มต้นมวลทั้งหมดอยู่นิ่ง เมื่อปล่อยให้ระบบเคลื่อนที่ สปริงจะคลายตัวและดันมวลให้เคลื่อนที่ออกจากกันและแยกออกจากปลายสปริง
กำหนดให้อัตราเร็วสุดท้ายของมวล $4M$ เท่ากับ $V$ เทียบกับพื้น และความเร็วเฉลี่ยของสปริงทั้งอันหลังคลายตัวเท่ากับ $u=\frac{aM}{bm+M}V$ เทียบกับพื้น
จงหาค่าของ $a$ และ $b$ เป็นตัวเลขทศนิยม 1 ตำแหน่ง โดยใช้จุลภาคคั่นระหว่างคำตอบทั้งสอง เช่น หากได้ $a=0.1$ และ $b=0.2$ ให้ตอบเป็น 0.1,0.2 ให้ประมาณว่าสปริงยืดหดอย่างสม่ำเสมอทั้งอัน อย่าลืมจัดรูปสมการให้ได้สัมประสิทธิ์ที่ต้องการ
เฉลย
ตอบ 1.5,0.5
จากข้อก่อนนี้ เมื่อเทียบกับกรณี $m$ มีค่าน้อยมาก นักเรียนสามารถตอบได้ทันทีว่า $a=1.5$ ส่วนค่าของ $b$ นั้นยังไม่สามารถตอบได้ทันที
ความเร็วเฉลี่ยของสปริงทั้งอันจะเท่ากับความเร็วของศูนย์กลางมวลสปริง
ให้ $V'$ เป็นความเร็วของมวล $M$ ไปทางขวา
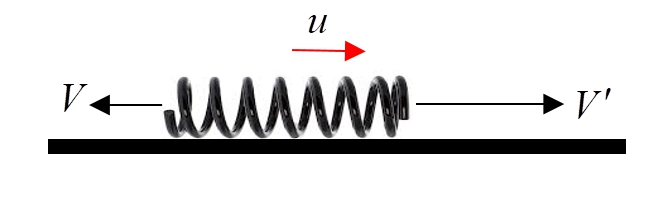
สมการการอนุรักษ์โมเมนตัมของมวลทั้งสาม
$4MV=mu+MV'$
สมการความเร็วสัมพัทธ์ระหว่างจุดกึ่งกลางและปลายทั้งสองข้าง
$V'-u=u+V$
แก้สมการได้ $u=\frac{3M}{m+2M}V = \frac{1.5M}{0.5m+M}V$
หมายเหตุ:
1. มีการสั่นของสปริงรอบจุด CM ของมันด้วย ดังนั้น พลังงานศักย์ตั้งต้น $\rightarrow$ พลังงานจลน์การเลื่อนตำแหน่งของมวลทั้งหมด + การสั่นของสปริง
2. เนื่องจากสปริงมีมวล การกำหนดให้มันยืดออกอย่างสม่ำเสมอ เป็นเพียงการประมาณ