คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
แชร์
ไม่ได้ส่งคำตอบ 
ยานอวกาศลำหนึ่งโคจรรอบโลกเป็นวงกลมที่มีอัตราเร็วคงที่ $v_0$ จากนั้นจุดจรวดเป็นระยะเวลาสั้นมาก ทำให้ความเร็วเพิ่มขึ้นเป็น $\beta v_0$ โดยไม่เปลี่ยนทิศความเร็วและ $\beta=1.05$ หลังจากนั้นปิดเครื่องยนต์จรวดและปล่อยให้ยานโคจรรอบโลกต่อไป
จงหาค่า eccentricity ของวงโคจรใหม่ ให้ตอบเป็นตัวเลขทศนิยม 4 ตำแหน่ง
จงหาค่า eccentricity ของวงโคจรใหม่ ให้ตอบเป็นตัวเลขทศนิยม 4 ตำแหน่ง
เฉลย
วงโคจรใหม่จะเป็นวงรี ที่มีระยะจากโลกตามสมการ
$r=\frac{a(1-e^2)}{1+e \cos \theta}$ เมื่อ $e$ เป็น eccentricity
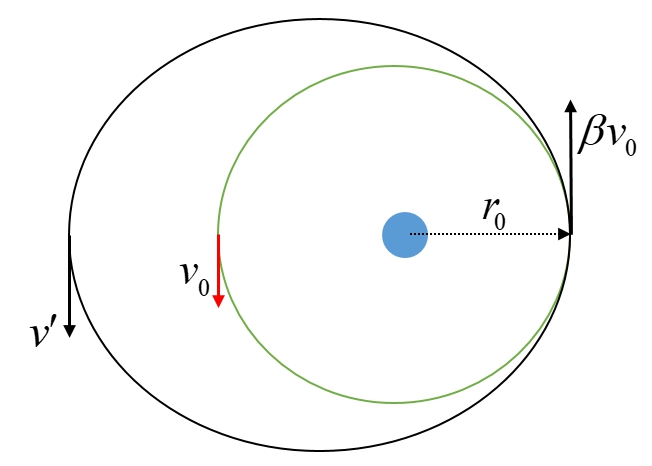
ให้ $r_0$ เป็นรัศมีของวงโคจรเดิม
ให้ $m$ เป็นมวลของยาน
ที่ตำแหน่งไกลสุดจากโลก มีระยะ $a(1+e)$ มีอัตราเร็ว $v'$
ที่ตำแหน่งใกล้สุดจากโลก มีระยะ $a(1-e) = r_0$ มีอัตราเร็ว $v_0$
การอนุรักษ์โมเมนตัมเชิงมุม
$m \beta v_0 r_0 = m v' a(1+e)$
การอนุรักษ์พลังงาน
$\frac{1}{2}m {(\beta v_0)}^2 - \frac{GMm}{r_0} = \frac{1}{2}m {v'}^2 - \frac{GMm}{a(1+e)}$
การเคลื่อนที่เป็นวงกลมก่อนหน้า
$\frac{GMm}{r_0^2} = \frac{m v_0^2}{r_0}$
ตัดตัวแปรอื่นๆออก จะได้ $e=\beta^2 - 1 = 0.1025$
หมายเหตุ:
การแข่ง Mini Olympiads รอบนี้นั้นตรวจได้เฉพาะคำตอบสุดท้ายเท่านั้น
แต่ในการแข่งขันโอลิมปิกวิชาการจริงนั้น นักเรียนจะได้คะแนนการแสดงวิธีทำในแต่ละขั้นตอนด้วย ไม่ใช่เฉพาะคำตอบสุดท้ายเท่านั้น