คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
ไม่ได้ส่งคำตอบ 
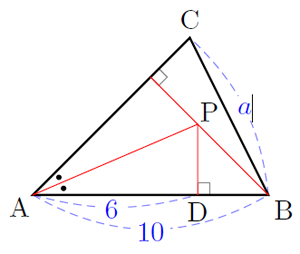
$\Delta \text{ABC}$ มีพื้นที่ $36$ ตารางหน่วย และ $\text{AB} = 10$ หน่วย
เส้นแบ่งครึ่งมุม $\text{A}$ ตัดเส้นส่วนสูงจากจุดยอด $\text{B}$ ที่จุด $\text{P}$
ให้ $\overline{\text{PD}} \bot \ \overline{\text{AB}}$ ที่จุด $\text{D}$ และ $\text{AD} = 6$ หน่วย
ถ้า $\text{BC} = a$ หน่วย จงหาค่าของ $a^2$
เส้นแบ่งครึ่งมุม $\text{A}$ ตัดเส้นส่วนสูงจากจุดยอด $\text{B}$ ที่จุด $\text{P}$
ให้ $\overline{\text{PD}} \bot \ \overline{\text{AB}}$ ที่จุด $\text{D}$ และ $\text{AD} = 6$ หน่วย
ถ้า $\text{BC} = a$ หน่วย จงหาค่าของ $a^2$
เฉลย
ตอบ 73
แนวคิด
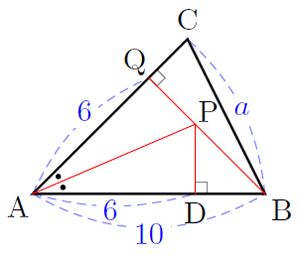
\(\Delta \text{APQ} \cong \Delta \text{APD} \Rightarrow \text{AQ} = \text{AD} = 6\)
จาก \(\Delta \text{PBD}\) จะได้ว่า \(\text{BQ} = \sqrt[]{10^2 - 6^2} = 8\)
\(\displaystyle{\frac{1}{2}} \cdot \text{BQ} \cdot \text{AC} = [\Delta \text{ABC}] = 36 \Rightarrow \text{AC} = 9\)
\(\therefore a^2 = \text{BQ}^2 + \text{QC}^2 = 8^2 + (9 - 6)^2 = 73\)