ข้อที่ 129

ตอบ 0.5,1.5

พิจารณาการสะท้อนครั้งที่ 1

ให้ภาพเกิดที่ตำแหน่ง $u$ ห่างจากกระจกอันบน

$\displaystyle{\frac{1}{d} + \frac{1}{u} = \frac{2}{R}}$

ภาพจากกระจกบนเป็นวัตถุให้กับกระจกล่าง ซึ่งเป็นไปได้ 2 กรณีคือ

1. ภาพจากกระจกบนเป็นภาพจริง

สมการของการสะท้อนกระจกล่าง $\displaystyle{\frac{1}{d-u} + \frac{1}{d} = \frac{2}{R}}$

2. ภาพจากกระจกบนเป็นภาพเสมือน (หลังกระจกบน)

สมการของการสะท้อนกระจกล่าง $\displaystyle{\frac{1}{d+u} + \frac{1}{d} = \frac{2}{R}}$

เมื่อแก้สมการทั้ง 2 กรณีร่วมกับการสะท้อนครั้งแรก

จะพบว่ามี 2 คำตอบคือ $d = \displaystyle{\frac{R}{2}}$ และ $d = \displaystyle{\frac{3R}{2}}$

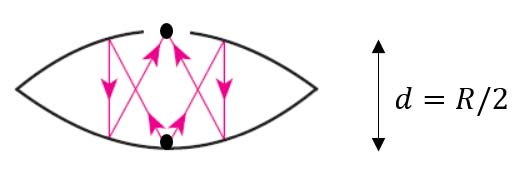
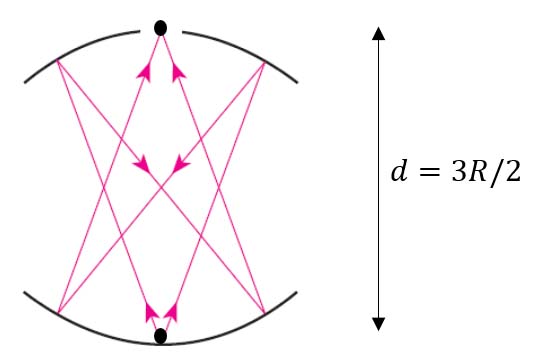
การเกิดภาพที่รูพอดี จะต้องเกิดจากการสะท้อนที่เป็นเลขคู่

หากมีการสะท้อนหลายครั้งมากขึ้น จะมีตำแหน่ง $d$ ที่เป็นไปได้มากขึ้น