คำตอบของทีม
ไม่ได้ส่งคำตอบ
ไม่ได้ส่งคำตอบ
คะแนน + โบนัสทำเร็ว
0.0
0.0
แชร์
ไม่ได้ส่งคำตอบ 
แกลแวนอมิเตอร์เป็นอุปกรณ์วัดไฟฟ้าประเภทหนึ่งที่มีเข็มชี้ติดอยู่กับขดลวดในสนามแม่เหล็ก
เมื่อปิดสวิตซ์ $\text{S}_1$ ให้กระแสไหลได้ พบว่าเข็มแกลแวนอมิเตอร์เบี่ยงไปเป็นมุม $\theta_0$ เมื่อปิดสวิตซ์ $\text{S}_2$ ด้วย (ปิดทั้งคู่) พบว่าเข็มแกลแวนอมิเตอร์เบี่ยงน้อยลงเป็นมุม $\frac{\theta_0}{2}$ หรือเพียงครึ่งหนึ่งของก่อนหน้านี้
กำหนดให้เซลล์ไฟฟ้ามีความต้านทานภายในน้อยมาก และความต้านทานภายในของแกลแวนอมิเตอร์มีค่าเท่ากับ $\frac{R_2(aR_1+bR_2)}{R_1+cR_2}$
จงหาค่าของ $a$, $b$ และ $c$ เป็นเลขจำนวนเต็ม โดยใช้เครื่องหมายจุลภาค (,) คั่นระหว่างคำตอบ หากมีค่าน้อยกว่าศูนย์ให้ใส่เครื่องหมายลบข้างหน้าตัวเลขนั้น
เมื่อปิดสวิตซ์ $\text{S}_1$ ให้กระแสไหลได้ พบว่าเข็มแกลแวนอมิเตอร์เบี่ยงไปเป็นมุม $\theta_0$ เมื่อปิดสวิตซ์ $\text{S}_2$ ด้วย (ปิดทั้งคู่) พบว่าเข็มแกลแวนอมิเตอร์เบี่ยงน้อยลงเป็นมุม $\frac{\theta_0}{2}$ หรือเพียงครึ่งหนึ่งของก่อนหน้านี้
กำหนดให้เซลล์ไฟฟ้ามีความต้านทานภายในน้อยมาก และความต้านทานภายในของแกลแวนอมิเตอร์มีค่าเท่ากับ $\frac{R_2(aR_1+bR_2)}{R_1+cR_2}$
จงหาค่าของ $a$, $b$ และ $c$ เป็นเลขจำนวนเต็ม โดยใช้เครื่องหมายจุลภาค (,) คั่นระหว่างคำตอบ หากมีค่าน้อยกว่าศูนย์ให้ใส่เครื่องหมายลบข้างหน้าตัวเลขนั้น
เฉลย
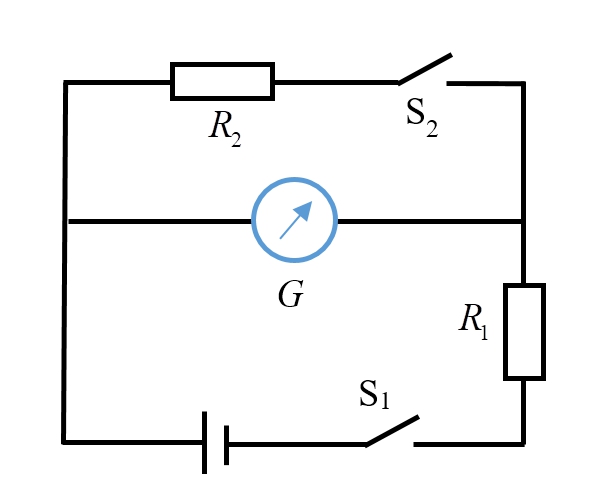
การเบี่ยงของเข็มขึ้นอยู่กับกระแสที่ไหลผ่าน $\text{G}$ ซึ่งกระแสนี้แปรผันกับศักย์ที่คร่อมมัน วิธีการหาความต้านทานนี้เรียกว่า Half Deflection Method
ให้ $E$ เป็น $emf$ ของเซลล์ไฟฟ้า และ $G$ เป็นความต้านทานของแกลแวนอมิเตอร์
ความต่างศักย์ที่คร่อม $\text{G}$ เมื่อปิดสวิตซ์ $\text{S}_1$ เท่ากับ $V_1=\frac{G}{G+R_1}E$
เมื่อปิดสวิตซ์ $\text{S}_2$ จะทำให้ $\text{G}$ ขนานกับ $R_2$ และมีความต้านทานรวมเท่ากับ $R_{||}=\frac{GR_2}{G+R_2}$
ความต่างศักย์ที่คร่อม $\text{G}$ เมื่อปิดสวิตซ์ $\text{S}_2$ ด้วย เท่ากับ $ V_2 = \frac{R_{||}}{R_{||}+R_1} E$
และ $V_1=2V_2$ แก้สมการได้ $G=\frac{R_1R_2}{R_1-R_2}$
หรือ $a=1$ และ $b=0$ และ $c=-1$
(หรือนักเรียนตั้งต้นคำนวณกระแสที่ผ่านแกลแวนอมิเตอร์ในตอนแรก และเทียบกับกระแสที่ลดลงครึ่งหนึ่งในตอนหลังก็ได้คำตอบเท่ากัน)